简答题

  1. 判断一个无向图是一棵树的条件是______
    有n个顶点，n-1条边的无向连通图
  2. 有向图 G 的强连通分量是指______
    有向图的极大强连通子图
  3. 一个连通图的______是一个极小连通子图
    生成树
  4. 具有 10 个顶点的无向图，边的总数最多为______
    45
  5. 若用 n 表示图中顶点数目，则有_______条边的无向图成为完全图
    n(n-1)/2
  6. 在有 n 个顶点的有向图中，若要使任意两点间可以互相到达，则至少需要______条弧
    n
  7. 在有 n 个顶点的有向图中，每个顶点的度最大可达______
    2(n-1)
  8. N 个顶点的连通图用邻接矩阵表示时,该矩阵至少有_______个非零元素
    2（N-1）
  9. 在图 G 的邻接表表示中，每个顶点邻接表中所含的结点数，对于无向图来说等于该顶点的______；对于有向图来说等于该顶点的______。
    度　　　出度
  10. 在有向图的邻接矩阵表示中，计算第 I 个顶点入度的方法是______
    第I列非零元素个数
  11. 已知一无向图 G=（V，E），其中 V={a,b,c,d,e } E={(a,b),(a,d),(a,c),(d,c),(b,e)}现用某一种图遍历方法从顶点 a 开始遍历图，得到的序列为 abecd，则采用的是______遍历方法
    深度优先
  12. 构造连通网最小生成树的两个典型算法是______
    普里姆（prim）算法和克鲁斯卡尔（Kruskal）算法
  13. 求图的最小生成树有两种算法，______算法适合于求稀疏图的最小生成树
    克鲁斯卡尔（Kruskal）
  14. Prim（普里姆）算法适用于求______的网的最小生成树；kruskal（克鲁斯卡尔）算法适用于求______的网的最小生成树。
    边稠密　　　　边稀疏
  15. 有向图 G 可拓扑排序的判别条件是______
    不存在环
  16. AOV 网中,结点表示______,边表示______。AOE 网中,结点表示______,边表示______。
    1）活动（2）活动间的优先关系（3）事件（4）活动边上的权代表活动持续时间
  17. 在 AOE 网中，从源点到汇点路径上各活动时间总和最长的路径称为______。
    关键路径
  18. 在 AOV 网 中，存在环意味着______，这是______的；对程序的数据流图来说，它表明存在______。
    1）某项活动以自己为先决条件（2）荒谬（3）死循环
  19. 有向图的邻接表存储如下：
    （1）画出其邻接矩阵存储；
    （2）写出图的所有强连通分量；
    （3）写出顶点 a 到顶点 i 的全部简单路径。
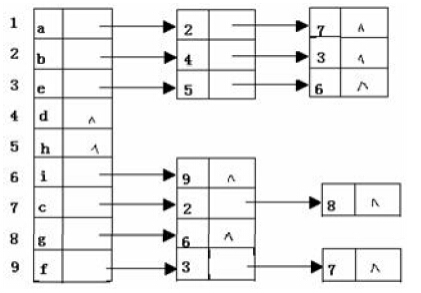    IT料理 (1) 略，注：邻接矩阵下标按字母升序:abcdefghi
    （2）强连通分量：（a），(d)，（h），(b，e，i，f，c，g）
    （3）顶点a到顶点i的简单路径： （a->b->e->i），(a->c->g->i)，(a->c->b->e->i)
  20. 首先将如下图所示的无向图给出其存储结构的邻接链表表示，然后写出对其分别进行深度，广度优先遍历的结果
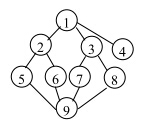    IT料理 邻接表略
    深度优先遍历序列：125967384
    宽度优先遍历序列：123456789
    注：（1）邻接表不唯一，这里顶点的邻接点按升序排列
    （2）在邻接表确定后，深度优先和宽度优先遍历序列唯一
    （3）这里的遍历，均从顶点1开始
  21. 下图是带权的有向图 G 的邻接表表示法，求：
    （1）以结点 V1 出发深度遍历图 G 所得的结点序列；
    （2）以结点 V1 出发广度遍历图 G 所得的结点序列；
    （3）从结点 V1 到结点 V8 的最短路径；
    （4）从结点 V1 到结点 V8 的关键路径。
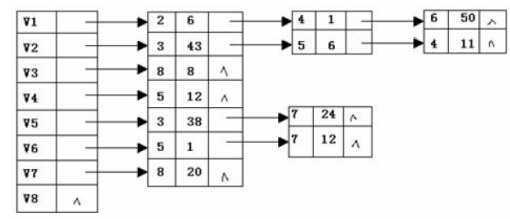    IT料理 （1）V1,V2,V3,V8,V5,V7,V4,V6
    （2）V1,V2,V4,V6,V3,V5,V7,V8
    （3）V1到V8最短路径56，路径为V1----V2----V5----V7----V8
    （4）V1到V8的关键路径是V1----V6----V5----V3----V8，长97。